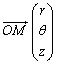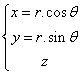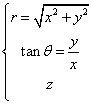|
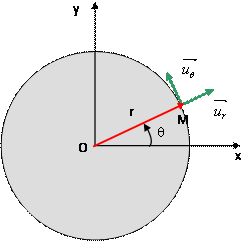
3. Coordonnées polaires
Ce système de coordonnées peut être utilisé pour les systèmes en rotation dans un plan. Les vecteurs unitaires sont
Les coordonnées polaires de M sont la coordonnée radiale r et la coordonnée angulaire q (angle polaire ou azimut) :
On peut écrire :
4. Coordonnées cylindriques
Ce système de coordonnées est une extension à 3 dimensions des coordonnées polaires. Il est utilisé pour étudier les problèmes à symétrie de révolution (par exemple : mouvement circulaire, rotation d’une roue autour de son axe).
La base unitaire directe est constituée par les vecteurs :
Si on suppose que le point M décrit un cercle de rayon r, à l’altitude OH, · ·
Les coordonnées cylindriques de M sont les coordonnées polaires r et θ , et la hauteur z :
On peut exprimer le vecteur
Si on connaît les coordonnées cylindriques d’un point, on peut exprimer ses coordonnées cartésiennes :
Inversement, on peut exprimer les coordonnées cylindriques à partir des coordonnées cartésiennes :
|