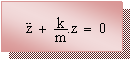2. Oscillations verticales d’un ressort

 

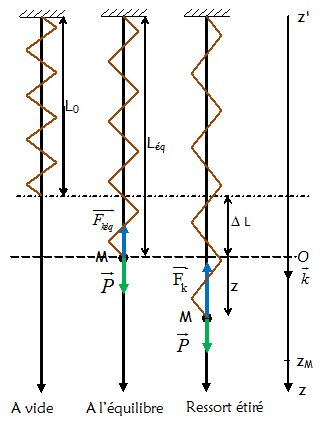
           On reprend le problème précédent, en position verticale. Cependant, ici, lorsque le système {M} est à l’équilibre, le ressort exerce une certaine tension car le ressort est allongé.

 

           On tire d’une longueur z_M sur le système par rapport à sa position d’équilibre puis on le lâche.

 

 

 

           On applique de la même façon le PFD :

 

           dépend de l’allongement global du ressort : (z+∆L), où ∆L = L_éq – L₀

 

           Projection selon z’z : 

  (2)

 

           Si on applique maintenant le PFD lorsque le ressort est à l’équilibre, on a :

 

           soit            P = F_kéq = k.∆L

 

           Cela permet de simplifier l’équation (2) :          soit

 

 

           On retrouve une équation différentielle du second ordre. La solution est du même type que pour le ressort horizontal. Avec les conditions initiales similaires, on trouve :

 

 

           Lorsque le ressort est en position verticale, il n’oscille plus autour de sa position au repos L₀ mais autour de sa position à l’équilibre L_éq = (L₀ + ∆L) lorsque la masse M est accrochée !

 

 

Remarque : en choisissant l’origine de l’axe (z’z) en ce point d’équilibre, on simplifie la résolution de l’équation différentielle.